논문 링크: https://arxiv.org/abs/2006.11239
참고한 유튜브 링크1: https://youtu.be/1j0W_lu55nc?si=tIa2ldDzrMt5Mf_h
참고한 유튜브 링크2: https://youtu.be/uFoGaIVHfoE?si=TUCkQUUcyOZy4PeQ
Abstract
- Diffusion probabilistic model을 이용한 고퀄리티 이미지 합성 결과를 보인다.
- 이는 비평형 열역학에서 얻은 아이디어
- DPM과 Langevin dynamics를 통한 denoising score matching 사이에 새로운 연결로 weighted variational bound를 설계
- 또한, autoregressive decoding의 생성으로 progressive lossy decompression scheme 사용
Introduction

- 기존에 GANs, Flows, VAEs, autoregressive models 등의 모델들이 이미지 및 음성 합성에 대해 좋은 결과를 보임
- 또한 energy-based modeling과 score matching도 많이 발전됨.
- 디퓨전 모델은 variational inference를 통해 훈련된 parameterized Markov chain이다.
- Diffusion process의 reverse를 학습한다.
- Diffusion process란 signal이 무너질 때까지 샘플링의 반대 방향으로 노이즈를 계속해서 추가하는 것
- Diffusion process가 작은 크기의 가우시안 노이즈라면, 샘플링 체인의 transition도 간단한 신경망 parameterization을 통하면 conditional 가우시안이라고 볼 수 있다.
- Diffusion Model은 정의하기 간단하고 학습이 효율적이지만, 이것이 높은 퀄리티의 샘플을 생성한다는 demo가 없었다.
- 본 논문에서는 디퓨전 모델이 현재의 생성 모델들에 비해 밀리지 않는 생성능력을 가졌음을 보인다.
- 또한, Diffusion에 특정한 parameterization을 적용하여, 이것이 학습 중의 여러 번의 노이즈 단계에 대한 annealed Langevin dynamics의 denoising score matching과 같음을 보인다.
- 다만, 디퓨전 모델이 퀄리티가 좋은 생성을 하지만, log likelihoods(모델이 데이터를 얼마나 잘 설명하는지)에 대해서는 다른 주된 생성모델들에 비해 경쟁력이 없다.
- DDPM의 lossless codelength가 감지하기 어려운 이미지의 디테일을 표현하는데 사용됐다.
- 디퓨전 모델의 샘플링이 Autoregressive model보다 더 일반화된 점진적 디코딩임을 보였다.
Background
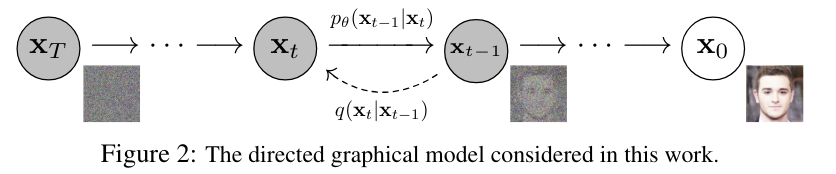
Diffusion model
Forward Process
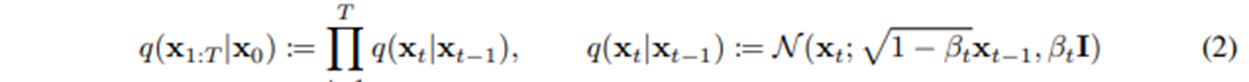
- Markov Chain
- Varince로 작은 가우시안을 더하고, mean은 조금 작아진다.
- variance를 1로 하기 위해 식 2의 variance의 계수가 beta_t일 때, mean의 계수가 저렇게 된다.
Reverse Process
- Forward process의 직접적인 reverse 과정은 intractable하기에 이를 approximate한 trainable network를 사용한다.
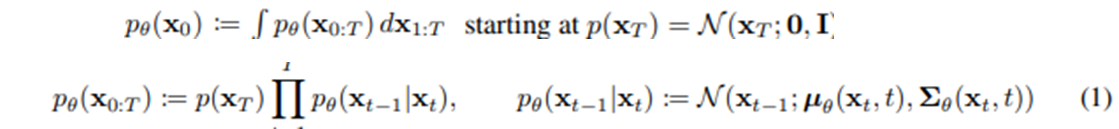
Diffusion kernel
- Diffusion 과정을 한번에 수행
- 위의 식 2번 참고

- 루트(alpha_bar)가 0이 되도록 (large T)를 설계했다 → N(x_T; 0, I)
Variational bound

- 위의 식을 이용하여 아래 식을 만들 수 있다.
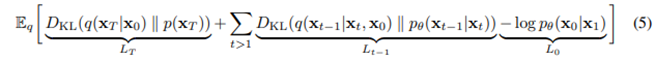
- 각 term은 Regularization, Denoising process 등을 의미
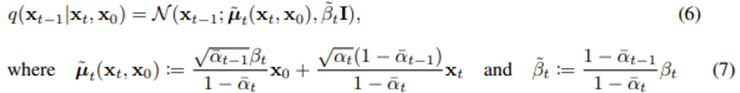
- q(x_t-1|x_t)는 x_0를 conditional하게 받아서 tractable해졌다.
- 6번 식을 사용하여, 5번식의 KL divergence 계산이 가능하다
- 아래 식은 가우시안 분포 사이의 KL divergence 계산 방법이다.
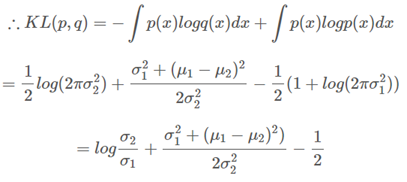
Diffusion Model Loss function 수식 유도
- 아래 과정은 식 (3), (5)를 유도한다.
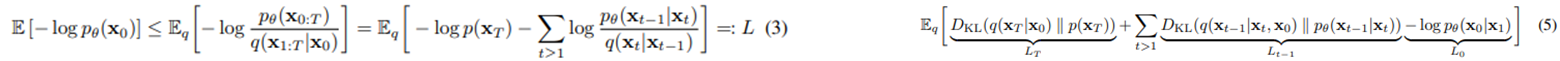
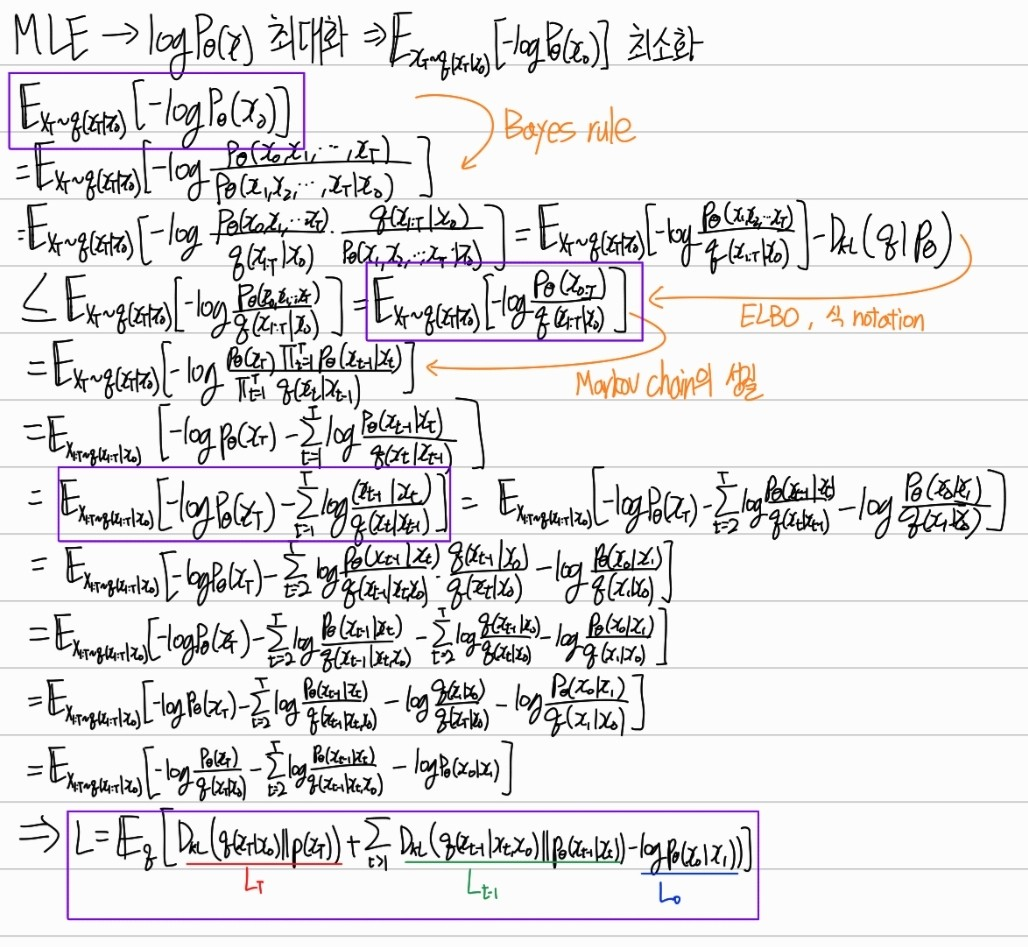
Diffusion models and denoising autoencoders
Forward process and L_T
- Beta_t를 learnable에서 fixed scheduling으로 변경
- q와 p 모두 동일한 가우시안 분포가 된다.
- 따라서 regularization term(기존에는 beta_t를 학습)은 필요가 없어져 삭제
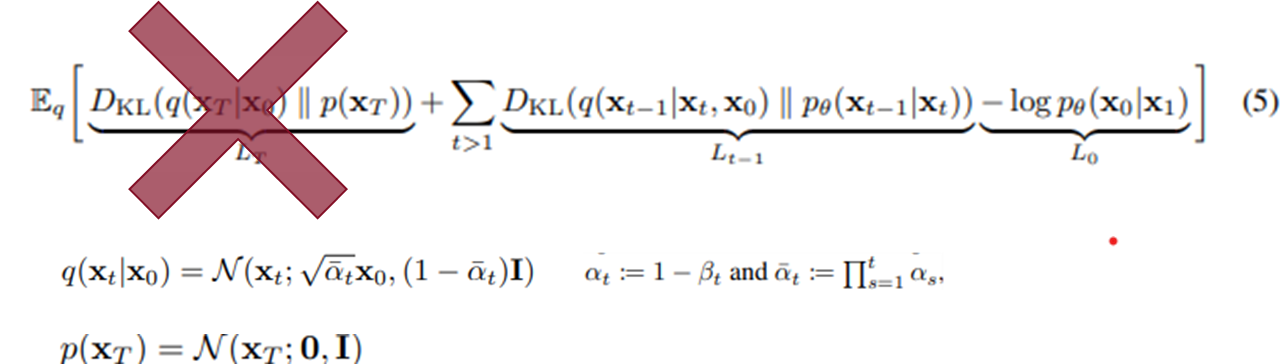
- 위의 식에서 볼 수 있듯이 첫번째 term에서 learnable한 파라미터가 없어졌다. → 따라서 해당 term을 없앨 수 있다.
Reverse process and L_1:T-1

- Rverse process를 위의 식들을 이용하여 정리하면 식 8이 나온다.
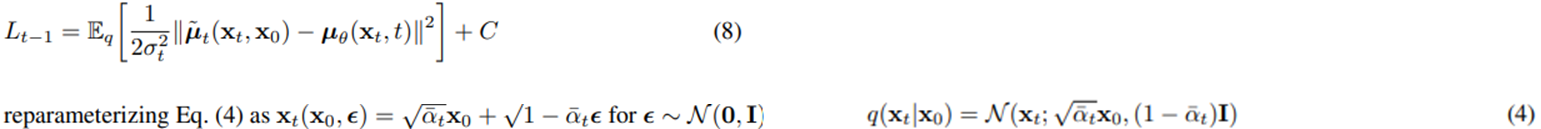
- 위 식을 식 8에 대입하여 아래의 식 10을 유도할 수 있다.
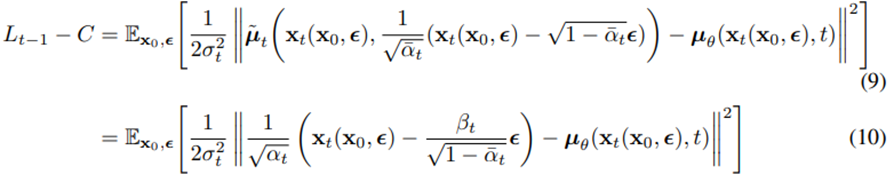
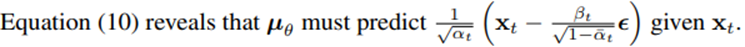
- 여기서 즉 mu_theta는 앞의 식만 예측하면 되고, 이는 즉, t 시점의 noise를 학습하는 것이다.
- 따라서 이를 Denoising Matching이라고 부른다.
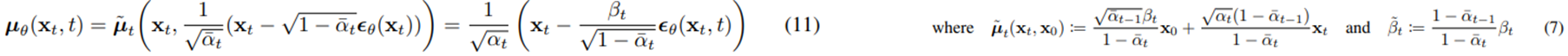
- 위 방식을 residual estimation의 한 방식이라고도 볼 수 있을 것이다.
- 이어서, 식 11을 식 10과 조합하여 식 12를 유도할 수 있다.
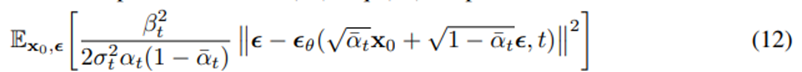
- 지금까지 전개한 식들을 이용한 Training 및 Sampling 알고리즘은 아래와 같다.

Reverse process decoder, and L_0
- L_0는 간단한 normal 분포로 볼 수 있다.
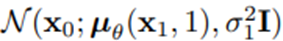
Simplified triaining objective
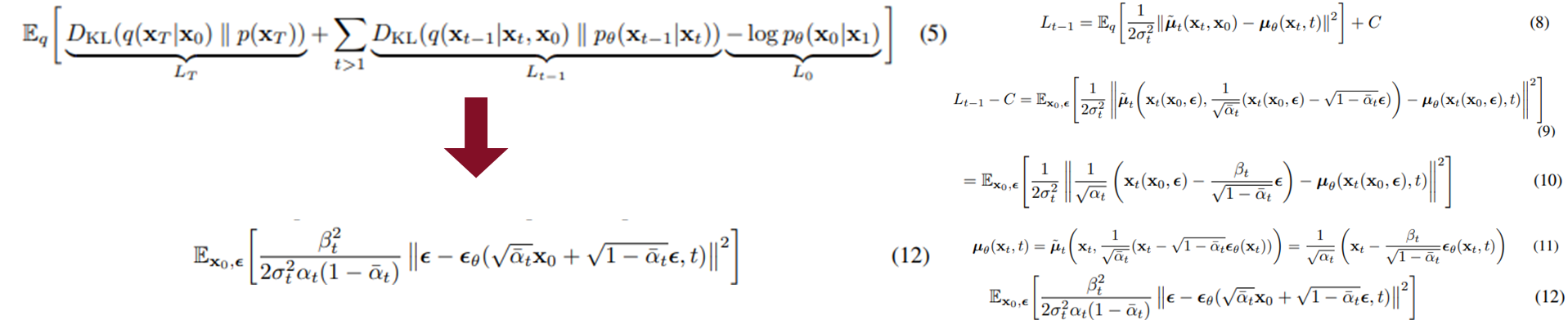
- 지금까지의 과정을 정리하여 training objective를 간단하게 만들 수 있다.
- beta_t가 고정되면서 regularization term과 variance term 제거
- mu_theta를 새롭게 정의하여 denoising matching form으로 변경
- 계수가 1이 되도록 설정 ⇒ 12번 식 탄생
- 위와 같은 loss function 간소화가 DDPM의 main contribution으로 볼 수 있다.
- 또한 위 처럼 식을 간소화 시킨 것은 inductive bias를 증가시킨 것으로도 볼 수 있을 것이다.
Experiments
Setting
- 모든 실험에서 T는 1000
- β_t 는 β_1=10^−4 에서 시작해 β_T=0.02로 선형적으로 증가
- x_T에서의 SNR은 매우 작게 설정
- 신경망은 U-Net 구조를 백본으로 사용
- 시간 t는 Transformer는 sinusoidal) positional embedding을 사용
Results
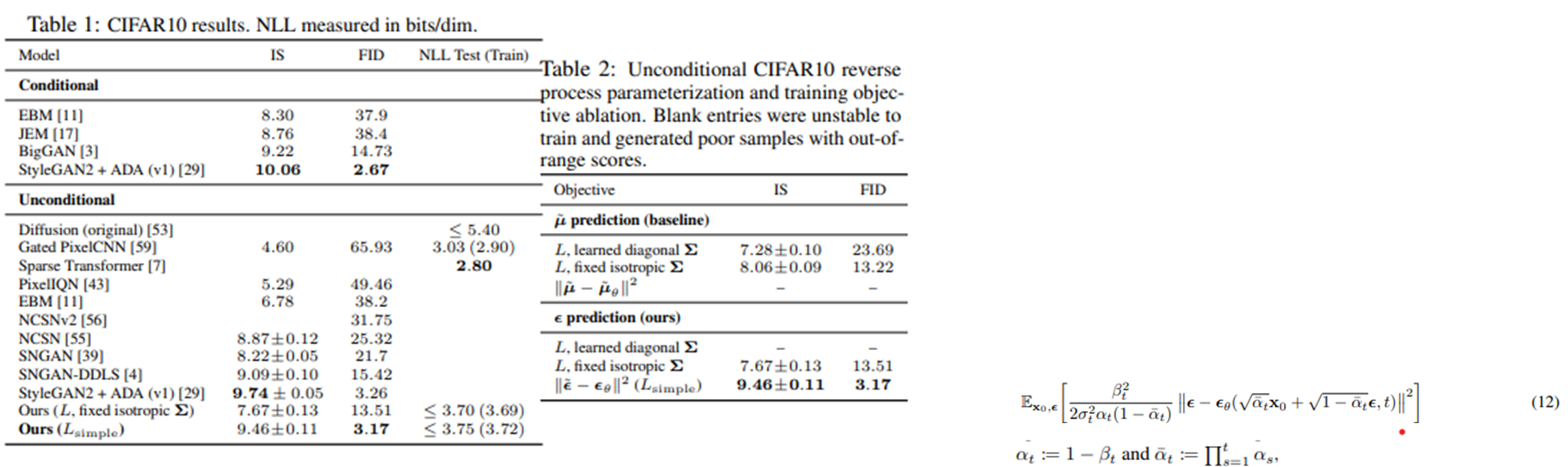
- Coefficient term을 제외하면서 NLL(Negative Log Likelihood)값은 약간 안좋아졌지만, 좋은 FID 값을 가지게 되었다.
- Noise가 심한 이미지(t가 클 때)의 denosing에 집중하게 했다고 이해할 수 있다. (learnable의 경우, large_t 시점의 계수가 더 작아졌다.)
- 총 4개의 loss식으로 실험
- mu 예측보다 noise를 예측한 것이 결과가 좋고, learnable보다 fixed의 결과가 좋다.
- 식을 단순화(inductive bias 증가)하니 더 좋은 결과가 있었다.

- 위 결과들은 각각 DDPM의 결과물, DDPM에서의 interpolation, progressive decoding(점진적 디코딩)을 보여준다.
